Long-run global economic growth
© TIM Garrett 2014
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
To what extent does our global economy rely on raw materials and energy? Can we decouple global economic innovation and growth from climate change?
The coming century is guaranteed to be one of immense change. Current exponential growth rates will see us double our energy demands in just 30 years, adding as much to our consumption capacity in our working lifetimes as we have in the entire history of civilization.
In the place of traditional macroeconomics, there is a new model for global economic growth that is based on physical principles. It looks at how energy and matter are transformed by the economy taken as a whole using a minimum of bells and whistles. Instead of focusing on what should be done in the future, it asks rather what will happen given the very general thermodynamic constraints that govern how systems of any stripe emerge, survive, and grow.
The core finding is that economic wealth or capital is not a static quantity that simply exists, but rather it requires continual energy consumption for its sustenance. Like a living organism, energy is required not just to grow civilization but also to maintain its current size. All components of civilization, whether human or physical, have no innate value in and of themselves; instead economic value is acquired through mutual connections: connections enable the circulations of matter that define humanity, requiring consumption of energy. Viewed very generally, total civilization wealth is directly tied to a global rate of energy consumption, or civilization’s power.
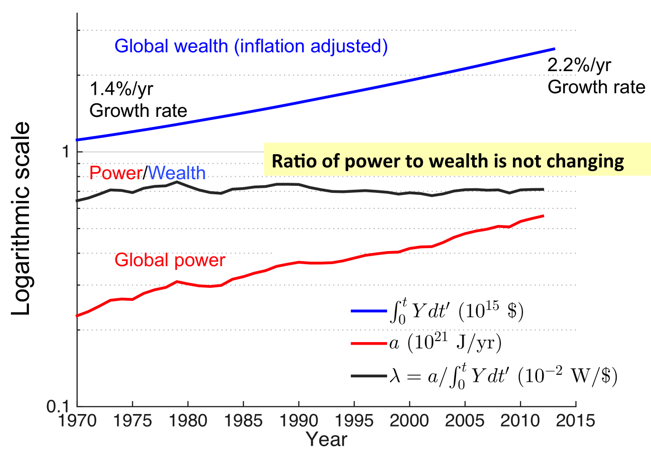
This is a testable hypothesis, one that is motivated by physics, and is supported by historical observations of the global economy. Summing wealth over all the world’s nations, 7.1 Watts is required to maintain every one thousand inflation-adjusted 2005 dollars of historically accumulated economic wealth.
To be clear, this relationship is not between energy and yearly economic output or GDP, nor is it to the more restrictive view of wealth as physical capital that can be found in traditional economic models. Instead, the constant relates current energy consumption to the summation of production not just over one year -- the GDP -- but over all of time. This quantity has a fixed relationship to current energy consumption that is independent of the year that is considered. As of 2010, civilization was powered by about 17 trillion Watts of power which supported about 2352 trillion dollars of collective global wealth. In 1970, civilization was younger, and both quantities were smaller by more than half. In the interim, energy consumption and wealth grew in tandem, but at variable rates that increased slowly from 1.4% per year to 2.2% per year.
If one really wants to relate energy to GDP, then the correct relationship is between GDP and the annual increase in the global power capacity. This relationship is much noisier than between energy consumption and wealth, but on average, adding every extra exajoule of global consumption capacity in a year enables 89 billion of year 2005 trillion USD of GDP, independent of the year that is considered.
Constants of proportionality are what provide a foundation for linking what initially seem to be two independent quantities (e.g. energy and frequency in quantum mechanics or energy and mass in relativity). Constants form the basis for all that follows. All other physical results are just math.
In the case of the constant of proportionality that relates civilization’s economic wealth to its rate of energy consumption, it tells us not just where we are today but it dramatically simplifies and constrains long-term estimates of where the global economy is headed. The constant ties economics to physics, so with physics, more robust economic forecasts become possible.
The most easily appreciated implication of the constant value is that sustaining the GDP will require that we constantly grow global power production capacity; or, sustaining long-run global GDP growth will require constantly accelerating growth of global power capacity, i.e. that the rate of increase must itself increase.
The question of growing wealth shifts from the traditional approach of looking to economic policy to one that is largely a matter of assessing the geological availability of fossil reserves: will we uncover new reserves faster than we deplete them or switch to renewables? If we can’t, what then? And if we can, what does growing fossil fuel consumption imply for our climate?
Many have pointed to energy efficiency as an escape from resource constraints, arguing that we can get more economic output with less consumption. This is true, but only locally. What arises from the constant λ is a seeming paradox: improving global energy efficiency benefits prosperity so that through a positive feedback, efficiency promotes faster global growth into the reserves that sustain us. With higher accessibility of these reserves, what follows is faster consumption of energy and raw materials.
The problem with accelerating economic growth is that carbon dioxide emissions also accelerate with their associated negative feedbacks on economic growth through climate change...unless the world switches away from fossil fuel power as fast as it grows: the equivalent of about one new nuclear reactor per day (approximately1 Gigawatt).
Ultimately, the goal of this work is to develop a robust model for the trajectory of civilization that is based to the greatest extent possible on the fundamentals of thermodynamics rather than the just-so stories of economic opinion. Only with testable principles can we eventually understand where we are headed.
What do you think an economic model should look like? Here’s my contact and a list of publications.
Economics About Physics of the economy What is wealth?
Energy, Innovation and growth Economic inertia Economic Forecasting Jevons' Paradox
Physics vs Mainsteam Economics Is Macroeconomics a Science? The economic heat engine
Economics and Climate GDP is not Wealth Are renewables the answer?
Is population growth a problem? Will growth transition to collapse?
What is your carbon footprint? Media Publications Presentations FAQ Criticisms
